Grafos
6 Grafos
Un grafo es una estructura de datos no lineal compuesta por nodos o vértices, conectados entre si por arcos o aristas. Los nodos representan objetos y los arcos las relaciones entre ellos.
Los grafos son un tipo de estructuras de datos donde cada elemento puede tener más de un sucesor, como los árboles, pero también poseer más de un predecesor. Esto hace que los grafos sean las estructuras más adecuadas para representar relaciones arbitrarias entre los elementos que los componen.
Los grafos tienen una terminología específica:
- Orden de un grafo: El número de nodos del grafo.
- Nodos adyacentes: Los nodos conectados por un arco.
- Grado de un nodo: En un grafo no dirigido: El número de arcos que inciden en el nodo. Eliminando los lazos. . La suma de los grados de los nodos es igual al doble del número de arcos.
- Semigrado interior de un nodo: En un grafo dirigido: Número de arcos de los nodos precedentes.
- Semigrado exterior de un nodo: En un grafo dirigido: Número de arcos a los nodos siguientes.
- Camino o circuito: Sucesión de nodos unidos por arcos.
- Camino simple: El camino en el que no se repite ningún arco.
- Longitud de un camino: El número de arcos que componen el camino. Para un grafo ponderado, es la suma de los pesos del camino. Un nodo independiente tiene longitud 0.
- Ciclo o camino cerrado o circuito: El camino en el que coinciden los nodos extremos. Y en el que no se repiten arcos.
- Bucle : Arco cuyos vértices inicial y final coinciden.
- Grafo conexo: Grafo no dirigido tal que para cualquier par de nodos existe al menos un camino que los une.
- Grafo fuertemente conexo: Grafo dirigido tal que para cualquier par de nodos existe un camino que los une.
- Grafo acíclico: Grafo que no tiene ciclos. Un grafo acíclico conectado se considera un árbol, y un grafo acíclico desconectado se denomina bosque.
- Camino o circuito Hamiltoniano: Aquel en el cual aparecen todos los nodos del grafo, pasando solo una vez por cada uno.
- Camino o circuito Euleriano: Aquel en el cual aparecen todos los arcos del grafo, sin importar que se visiten los nodos más de una vez.
Existen diferentes tipos de grafos, pero en nuestro caso vamos a trabajar tan solo con tres tipos:
- Grafo no dirigido: Grafo que tiene un conjunto de nodos y un conjunto de arcos entre los nodos donde el orden de los nodos conectados no es importante. Los arcos se consideran bidireccionales.
- Grafo dirigido o digrafo: Los arcos que conectan los nodos son unidireccionales. El arco se representa con una flecha, que indica la dirección del nodo origen al nodo destino.
- Grafo ponderado: Grafo en el que a cada arista se le asocia un valor numérico o peso.
6.1 Recorridos
Los recorridos en grafos se aplican de manera similar a los recorridos en árboles, la idea es visitar todos los nodos que lo forman, moviéndose por los arcos, para lo cuál se debe llevar la cuenta de los nodos visitados y no visitados.
Hay dos enfoques básicos:
Recorrido primero en profundidad (Depth-First Search - DFS).
Es una generalización del recorrido en preorden de un árbol.
- A partir de un nodo dado se localizan sus nodos adyacentes y para cada uno de ellos se inicia nuevamente el recorrido DFS.
- Es necesario llevar la cuenta de los nodos visitados (y no visitados).
- El recorrido no es único: depende del vértice inicial y del orden de visita de los vértices adyacentes.
Se hace uso de una pila para almacenar los nodos no visitados.
Recorrido primero en anchura o amplitud (Breadth-First Search - BFS).
Es una generalización del recorrido por niveles de un árbol.
El recorrido en anchura es una estrategia aplicable indistintamente al caso de grafos dirigidos y no dirigidos.
- A partir de un nodo dado se visitan todos sus nodos adyacentes.
- A continuación, los adyacentes a éstos.
- Y así sucesivamente.
Se hace uso de una cola para almacenar los nodos no visitados.
6.1.1 Extensión de coste mínimo
En un grafo es fácil que haya caminos redundantes, así, podemos llegar por diferentes arcos de un nodo a otro. Si en un grafo conexo eliminamos los caminos redundantes, seguirá siendo conexo, si, además, nos quedamos con los caminos de menor coste habremos simplificado el grafo.
En el caso de los grafos ponderados resulta interesante encontrar el recorrido de peso mínimo entre dos nodos. El algoritmo de Dijkstra es el método general de búsqueda de este tipo de recorrido.
6.2 Representaciones
Los grafos se pueden representar mediante dos estructuras de datos distintas:
- Matriz de adyacencia . Consiste en una tabla de tamaño VxV, en que la posición m[i][j] tendrá como valor 1 si existe un arco del nodo i al nodo j. En caso contrario, el valor será 0. Cuando se trata de grafos ponderados en lugar de 1 el valor que tomará será el peso del arco. Si el grafo es no dirigido debe marcarse con un 1 (o con el peso) tanto la entrada m[i][j] como la entrada m[j][i].
- Lista de adyacencia . Cada nodo A tendrá una lista asociada con los nodos a los que está unido, así, habrá una referencia al nodo B si A y B tienen un arco que los une. Si el grafo es no dirigido, en la lista de B aparecerá la correspondiente referencia al nodo A. En el caso de que el grafo sea ponderado llevaran el peso asociado a cada arco.
La lista de adyacencia es un modelo dinámico, lo que permite cambiar el número de nodos sin necesidad de volver a crear una nueva matriz de adyacencia.
En los siguientes desarrollos vamos a emplear las listas de adyacencia en forma de diccionario de Python, donde las claves serán los nodos y los valores una lista de nodos adyacentes al nodo de la clave.
grafo = { <nodo>: [<nodos_adyacentes>]}
En el caso de grafos ponderados, cada nodo adyacente de la lista estará formado por una tupla de la forma:
(<nodo_adyacente>, <peso>)
El empleo de un diccionario nos va a facilitar las operaciones sobre el grafo, como listar nodos, obtener adyacencias, eliminar nodos, etc. Aunque debemos tener en cuenta que la implementación con listas de adyacencia determina el tratamiento del grafo, por lo que nos encontramos que un mismo grafo con un orden distinto de los arcos en la entrada producirá listas de adyacencia diferentes y por ello el orden en que los nodos se procesen producirá variaciones en los resultados.
Consideraremos el mínimo de operaciones a realizar sobre un TAD grafo:
- Creación: Realizar operaciones de inicialización del objeto y obtener un nuevo objeto del tipo grafo.
- Inserción: Introducir nuevos elementos en el objeto.
- Añadir nodo: Añade el nuevo nodo si no estaba ya en el grafo.
- Añadir arco: Añade un arco entre dos nodos del grafo. Si no existe alguno de los nodos se añadirá de forma implícita.
- Borrado: Funciones para eliminar o alterar el contenido del objeto.
- Eliminar nodo: Borra el nodo y los arcos del nodo eliminado.
- Eliminar arco: Borra el arco que relacionaba los nodos.
- Consulta: Realizar funciones que devuelven un valor en función de algún parámetro.
- Buscar caminos mínimos
- Comprobar si el grafo está vacío.
- Comprobar si existe un nodo.
- Comprobar si dos nodos son adyacentes.
En el caso de grafos ponderados debemos incluir el peso en la operación de Añadir arco.
6.3 Grafo no dirigido
Los grafos no dirigidos tienen un conjunto de nodos y un conjunto de arcos entre los nodos donde el orden de los nodos conectados no es importante.
Los arcos se consideran bidireccionales, así, en el caso de dos nodos unidos por un arco, es posible pasar de uno a otro y viceversa. Como vamos a representar los grafos en la implementación mediante una lista de adyacencias, cada par de nodos ayacentes llevarán en su lista la referencia al nodo al que está unido.
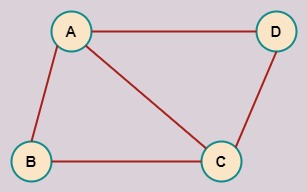
Grafo no dirigido
La representación del grafo de la imagen, como un diccionario de Python con sus listas de adyacencia, sería:
grafo = {'A': ['B', 'C', 'D'],
'B': ['A', 'C'],
'C': ['A', 'B', 'D'],
'D': ['A', 'C']}
Al ser un grafo no dirigido vemos que el nodo A contiene en su lista el nodo B, y en el nodo B aparece también el nodo A.
Las operaciones que vamos a definir sobre los grafos no dirigidos son:
| Método | Descripción |
|---|---|
| g = Graph() | Crea y devuelve un grafo vacío. |
| g.nodes() | Devuelve los nodos del grafo como una lista. |
| g.edges() | Devuelve los arcos del grafo como una lista de tuplas (orige, destino). |
| g.isolatedNodes() | Devuelve una lista de los nodos aislados. |
| g.order() | Devuelve el número de nodos del grafo. |
| g.size() | Devuelve el número de aristas del grafo. |
| g.degree(node) | Devuelve el número de aristas que conectan con el nodo indicado.
Los lazos se cuentan doblemente. Si el grafo está vacío devuelve -1. |
| g.Delta() | Devuelve el grado máximo. |
| g.addNode(node) | Inserta un nodo en el grafo. |
| g.removeNode(node) | Elimina un nodo del grafo. |
| g.addEdge(edge) | Inserta un arco entre los nodos indicados. Si no existe alguno de los nodos se añade de forma implícita. El arco es una lista con los nodos que une. |
| g.removeEdge(edge) | Elimina una arista entre nodos. |
| g.DFS(node) | Recorrido en profundidad desde el nodo indicado. Equivale al recorrido en preorden de un árbol. |
| g.BFS(node) | Recorrido en anchura desde el nodo indicado. Equivalente al recorrido de un árbol por niveles. |
| g.findPaths(start, end) | Devuelve todos los caminos entre dos nodos. |
| g.shortestPath(start, end) | Devuelve el camino más corto entre dos nodos. |
| g.isEmpty() | Devuelve True si el grafo está vacío, en caso contrario False. |
| g.existNode(node) | Devuelve True si el nodo está en el grafo, en caso contrario False. |
| g.existEdge(edge) | Devuelve True si existe el arco en el grafo (si los nodos son adyacentes), en caso contrario False. |
Dispondremos además de los métodos especiales:
| Método | Descripción |
|---|---|
| __init__(self) | Constructor, crea un grafo no dirigido vacío por defecto.
Se puede proporcionar un diccionario con el que se crea el grafo inicial. |
| __repr__(self) | Devuelve una representación formal del contenido del grafo. |
| __iter__(self) | Iterador para recorrer todos los nodos del grafo, con sus arcos, uno tras otro en el orden en que esté almacenado. |
Crearemos una clase con los métodos necesarios para implementar nuestro grafo no dirigido.
# grafo no dirigido
# admite lazos
class Graph():
# Constructor, por defecto crea un diccionario vacío
# El grafo se presenta como un diccionario de la forma
# {nodo: [arcos]}
# arcos es una lista de los nodos adyacentes
def __init__(self, graph={}):
self.graph = graph
# Devuelve una representación formal del contenido del grafo
def __repr__(self):
nodes = ''
for node, edges in self.graph.items():
nodes += f'{node}: {edges}\n'
return nodes
# Iterador para recorrer todos los nodos del grafo
def __iter__(self):
self.iter_obj = iter(self.graph)
return self.iter_obj
# Devuelve los nodos del grafo como una lista
def nodes(self):
return list(self.graph.keys())
# Devuelve los arcos del grafo como una lista de tuplas
# (nodo_origen, nodo_destino)
def edges(self, node=None):
if node:
if self.existNode(node):
return [(node, e) for e in self.graph[node]]
else:
return []
else:
return [(n, e) for n in self.graph.keys() for e in self.graph[n]]
# Devuelve una lista de los nodos aislados
def isolatedNodes(self):
return [node for node in self.graph if not self.graph[node]]
# Devuelve el número de nodos del grafo
def order(self):
return len(self.graph)
# Devuelve el número de arcos del grafo
def size(self):
arcs = []
for node, edges in self.graph.items():
for edge in edges:
sorted_edge = sorted([node, edge])
if sorted_edge not in arcs:
arcs.append(sorted_edge)
return len(arcs)
# Devuelve el número de arcos que conectan con el nodo
# Los lazos se cuentan doblemente
def degree(self, node):
if self.graph == {}:
return -1 # grafo vacío
degree = len(self.graph[node])
if node in self.graph[node]:
degree += 1 # existe un lazo
return degree
# Devuelve el grado máximo
def Delta(self):
if self.graph == {}:
return -1 # grafo vacío
degrees = [self.degree(node) for node in self.graph]
degrees.sort(reverse=True)
return degrees[0]
# Inserta un nodo en el grafo
def addNode(self, node):
# Si el nodo no está en el grafo,
# se añade al diccionario con una lista vacía
if node not in self.graph:
self.graph[node] = [] # nodo aislado
# Elimina un nodo del grafo
# Primero elimina todos los arcos del nodo
def removeNode(self, node):
if node in self.graph:
edges = list(self.graph[node])
for edge in edges:
self.removeEdge((node, edge))
self.graph.pop(node)
# Inserta una arco entre los nodos indicados
# El arco es una lista con los nodos que une
def addEdge(self, edge):
n1, n2 = tuple(edge)
# Se crean arcos del nodo1 al nodo2 y viceversa
for n, e in [(n1, n2), (n2, n1)]:
if n in self.graph:
if e not in self.graph[n]:
self.graph[n].append(e)
if n == e:
break # es un lazo
else:
self.graph[n] = [e] # no existe el nodo, se inserta
# Elimina un arco entre nodos
# El arco es una lista con los nodos que une
def removeEdge(self, edge):
n1, n2 = tuple(edge)
for n, e in [(n1, n2), (n2, n1)]:
if n in self.graph:
if e in self.graph[n]:
self.graph[n].remove(e)
# Recorrido en profundidad (Depth First Search)
# comienza en un nodo del grafo y
# comprueba a todo lo largo de cada arco antes de retroceder
def DFS(self, node):
visited = [node] # lista de visitados
stack = [node] # pila a tratar
while stack: # mientras haya nodos en la pila
current = stack.pop() # sacar nodo de la pila
if current not in visited: # si no ha sido visitado
visited.append(current) # añadir a visitados
for e in self.graph[current]: # para cada nodo adyacente
if e not in visited: # si no ha sido visitado
stack.append(e) # añadir a la pila
return visited # devolver el recorrido
# Recorrido en anchura (Breadth-First Search)
# comienza en un nodo del grafo y
# comprueba los nodos adyacentes en el nivel actual
# antes de pasar al siguiente nivel del grafo
def BFS(self, node):
visited = [node] # lista de visitados
queue = [node] # cola a tratar
while queue: # mientras haya nodos en la cola
current = queue.pop(0) # sacar nodo de la cola
if current not in visited: # si no ha sido visitado
visited.append(current) # añadir a visitados
for e in self.graph[current]: # para cada nodo adyacente
if e not in visited: # si no ha sido visitado
queue.append(e) # añadir a la cola
return visited # devolver el recorrido
# Devuelve todos los caminos entre dos nodos
def findPaths(self, start, end, path = []):
if start not in self.graph or end not in self.graph:
return []
path = path + [start]
if start == end:
return [path]
paths = []
for node in self.graph[start]:
if node not in path:
newpaths = self.findPaths(node, end, path)
for subpath in newpaths:
paths.append(subpath)
return paths
# Devuelve el camino más corto entre dos nodos
# camino más corto == menos nodos
def shortestPath(self, start, end):
path = sorted(self.findPaths(start, end), key = len)
return path[0] if path else []
# Consulta si el grafo está vacío
def isEmpty(self):
return self.graph == {}
# Consulta si el nodo existe en el grafo
def existNode(self, node):
return node in self.graph.keys()
# Consulta si el arco existe en el grafo
def existEdge(self, edge):
n1, n2 = tuple(edge)
return (n1, n2) in self.edges(n1) or (n2, n1) in self.edges(n2)
Describimos a continuación los métodos de nuestra implementación.
- __init__(self, graph={})
- El constructor del grafo crea un grafo vacío por defecto. Se puede pasar un grafo como una lista de adyacencia en forma de diccionario de Python, donde las claves del diccionario son los nodos y los valores son los arcos como una lista de nodos a los que se enlaza desde el nodo clave.
- __repr__(self)
- El método de representación del grafo como una relación de nodos con una lista adjunta de sus nodos adyacentes.
- __iter__(self)
- El iterador para recorrer los nodos del grafo nos hace entrega de un nodo cada vez que se le llame.
- nodes(self)
- Devuelve una lista con los nodos del grafo.
- edges(self, node=None)
-
Devuelve una lista de tuplas con los arcos del grafo.
Si se proporciona un nodo, devuelve los arcos que parten de ese nodo.
Si el nodo no existe, devuelve una lista vacía.
- isoladedNodes(self)
- Devuelve una lista con los nodos aislados del grafo.
- order (self)
- Devuelve el número de nodos del grafo.
- size(self)
- Devuelve el número de arcos del grafo.
- degree(self, node)
-
Devuelve el número de arcos que conectan con el nodo.
Si hay lazos se cuenta por dos.
Si el grafo está vacío se devuelve -1.
- Delta(self)
- Devuelve el grado máximo del grafo.
- addNode(self, node)
-
Inserta el nodo en el grafo.
Si el nodo no existe se añade al diccionario con una lista vacía de adyacencias.
Si el nodo ya existe, se ignora la orden.
- removeNode(self, node)
-
Elimina un nodo del grafo.
Si el nodo existe, se eliminan primero todas las referencias al nodo en las listas de adyacencia de los demás nodos. A continuación se elimina el nodo del diccionario.
Si el nodo no existe, se ignora la orden.
- addEdge(self, edge)
-
Inserta un arco entre los nodos indicados. El parámetro arco (edge) es una lista con los nodos que están relacionados.
Al ser un grafo no dirigido se crean arcos entre ambos nodos.
Si no existe alguno de los nodos se inserta en el diccionario con el otro nodo en su lista de adyacencia.
- removeEdge(self, edge)
-
Elimina un arco entre los nodos indicados. El parámetro arco (edge) es una lista con los nodos que están relacionados.
Se elimina de la lista de adyacencia de cada nodo el otro nodo al que está conectado.
- DFS(self, node)
-
Devuelve el recorrido en profundidad (Depth First Search) del grafo a partir del nodo indicado.
El recorrido comienza en un nodo del grafo y se comprueba a todo lo largo de cada arco antes de retroceder.
Se hace uso de una pila para almacenar los nodos pendientes de tratar.
- BFS(self, node)
-
Devuelve el recorrido en anchura (Breadth First Search) del grafo a partir del nodo indicado.
Comienza en un nodo del grafo y comprueba los nodos adyacentes en el nivel del nodo, antes de pasar al siguiente nivel del grafo.
Se hace uso de una cola para almacenar los nodos pendientes de tratar.
- findPaths(self, start, end, path = [])
- Devuelve una lista de listas con todos los caminos existentes entre los nodos inicio (start) y fin (end).
- shortestPath(self, start, end)
-
Devuelve el camino más corto entre dos nodos. Se entiende el camino más corto como el que pasa por menos nodos.
Se hace uso del método findPaths(). Si hay más un camino que cumple la condición se devuelve el primero que proporciona el procedimiento.
- isEmpty(self)
- Devuelve True si el grafo está vacío. En caso contrario False.
- existNode(self, node)
- Devuelve True si el nodo está en el grafo. En caso contrario False.
- existEdge(self, edge)
-
Devuelve True si el arco existe en el grafo. En caso contrario False. Se comprueba la existencia de un arco en los dos sentidos.
El parámetro arco (edge) es una lista con los nodos que están relacionados.
Construimos un script para probar nuestro módulo de tratamiento de grafos no dirigidos. Los comentarios en cada sentencia son suficientemente descriptivos.
import grafo as GR
# Grafo ejemplo con listas de adyacencia
grafo = {'A': ['B', 'C', 'D'],
'B': ['A', 'C'],
'C': ['A', 'B', 'D'],
'D': ['A', 'C']}
def testGrafo():
g = GR.Graph(grafo) # Crear el grafo con el diccionario de ejemplo
print('Grafo')
print(g) # Visualizar el grafo
print('Iteración')
for n in g: # Iterar sobre los nodos y arcos del grafo
print(n)
print(g.edges(n))
print('Nodos:', g.nodes()) # Visualizar todos los nodos
print('Arcos:', g.edges()) # Visualizar todos los arcos
print('Arcos desde el nodo C:', g.edges('C')) # Arcos desde un nodo
print('\nComprobaciones')
print('Vacío:', g.isEmpty()) # Comprobar si grafo vacío
print('Existe nodo A:', g.existNode('A')) # Comprobar si existe nodo
print('Existe nodo Z:', g.existNode('Z'))
print('Existe arco A-C:', g.existEdge(['A', 'C'])) # Comprobar arco
print('Existe arco A-Z:', g.existEdge(['A', 'Z']))
print('\nAñadir nodos y arcos')
g.addNode('E') # Añadir nodo
g.addEdge(['E', 'A']) # Añadir arco
g.addNode('F')
g.addEdge(['F', 'F'])
g.addEdge(['A', 'B'])
g.addEdge(['G', 'B'])
g.addEdge(['B', 'B'])
g.addEdge(('B', 'F'))
print('Grafo resultante')
print(g)
print('Medidas')
print('Grado de B:', g.degree('B')) # Obtener grado de un nodo
print('Grado de D:', g.degree('D'))
print('Delta:', g.Delta()) # Obtener Delta del grafo
print('Orden:', g.order()) # Obtener orden
print('Tamaño:', g.size()) # Obtener tamaño
print('\nRecorridos')
print("DFS('A'):", g.DFS('A')) # Recorrido DFS
print("BFS('A'):", g.BFS('A')) # Recorrido BFS
# Obtener todos los caminos posibles entre dos nodos
print('Caminos de A a C:', g.findPaths('A', 'C'))
# Obtener el camino más corto entre dos nodos
print('Más corto de A a C:', g.shortestPath('A', 'C'))
print('\nEliminar arcos y nodos')
g.removeEdge(['B', 'B']) # Eliminar arco
g.removeNode('B') # Eliminar nodo
g.removeEdge(['G', 'A'])
g.removeNode('Z') # Eliminar nodo inexistente
g.removeEdge(['B', 'Z']) # Eliminar arco inexistente
print('Grafo resultante')
print(g)
print('Nodos aislados:', g.isolatedNodes()) # Visualizar nodos aislados
if __name__ == '__main__':
testGrafo()
El resultado de la ejecución del programa de prueba es:
Grafo
A: ['B', 'C', 'D']
B: ['A', 'C']
C: ['A', 'B', 'D']
D: ['A', 'C']
Iteración
A
[('A', 'B'), ('A', 'C'), ('A', 'D')]
B
[('B', 'A'), ('B', 'C')]
C
[('C', 'A'), ('C', 'B'), ('C', 'D')]
D
[('D', 'A'), ('D', 'C')]
Nodos: ['A', 'B', 'C', 'D']
Arcos: [('A', 'B'), ('A', 'C'), ('A', 'D'), ('B', 'A'), ('B', 'C'), ('C', 'A'), ('C', 'B'), ('C', 'D'), ('D', 'A'), ('D', 'C')]
Arcos desde el nodo C: [('C', 'A'), ('C', 'B'), ('C', 'D')]
Comprobaciones
Vacío: False
Existe nodo A: True
Existe nodo Z: False
Existe arco A-C: True
Existe arco A-Z: False
Añadir nodos y arcos
Grafo resultante
A: ['B', 'C', 'D', 'E']
B: ['A', 'C', 'G', 'B', 'F']
C: ['A', 'B', 'D']
D: ['A', 'C']
E: ['A']
F: ['F', 'B']
G: ['B']
Medidas
Grado de B: 6
Grado de D: 2
Delta: 6
Orden: 7
Tamaño: 10
Recorridos
DFS('A'): ['A', 'E', 'D', 'C', 'B', 'F', 'G']
BFS('A'): ['A', 'B', 'C', 'D', 'E', 'G', 'F']
Caminos de A a C: [['A', 'B', 'C'], ['A', 'C'], ['A', 'D', 'C']]
Más corto de A a C: ['A', 'C']
Eliminar arcos y nodos
Grafo resultante
A: ['C', 'D', 'E']
C: ['A', 'D']
D: ['A', 'C']
E: ['A']
F: ['F']
G: []
Nodos aislados: ['G']
6.4 Grafo dirigido o digrafo
Un grafo dirigido o dígrafo es aquel en el que los arcos que unen nodos tienen un único sentido. El arco va desde el nodo origen al nodo destino. Decimos que el nodo origen precede al nodo destino, mientras que el nodo destino sucede al nodo origen. El arco se representa gráficamente con una flecha, que indica la dirección del nodo origen al nodo destino
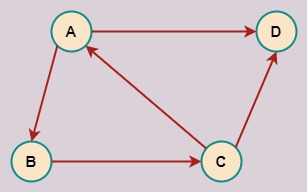
Grafo dirigido
La representación del grafo dirigido de la imagen, como un diccionario de Python, donde los nodos precedentes mantienen la lista de los nodos destino, es:
grafo = {'A': ['B', 'D'],
'B': ['C'],
'C': ['A', 'D'],
'D': []}
Al ser un grafo dirigido vemos que el nodo A contiene en su lista el nodo B, ya que la flecha nos indica que el nodo A es el precedente del nodo B, mientras que en el nodo B no aparece el nodo A.
Definiremos dos operaciones específicas para los grafos dirigidos.
| Método | Descripción |
|---|---|
| outDegree(node) | Devuelve el semigrado exterior del nodo indicado. El número de arcos a los nodos siguientes. |
| inDegree(node) | Devuelve el semigrado interior del nodo indicado. El número de arcos de los nodos precedentes. |
Vamos realizar la implementación empleando la clase Graph() que creamos en el punto anterior. Haremos uso de la herencia de los métodos correspondientes de la clase Graph(), reescribiendo aquellos métodos que hacian uso de la posibilidad de bireccionalidad de los arcos, que ahora no tenemos.
# Grafo dirigido
import grafo as GR
class DirectedGraph(GR.Graph):
# Constructor, por defecto crea un diccionario vacío
# El grafo se presenta como un diccionario de la forma
# {nodo: [arcos]}
# arcos es una lista de los nodos siguientes al nodo
def __init__(self, graph={}):
super().__init__(graph)
# Elimina un nodo del grafo
# Elimina todos los arcos desde otros nodos
def removeNode(self, node):
if node in self.graph:
nodes = list(self.graph)
for n in nodes:
if node in self.graph[n]:
self.graph[n].remove(node)
self.graph.pop(node)
# Inserta una arco entre los nodos indicados
# La arco es una lista con el nodo origen y destino
# Si no existe alguno de los nodos lo inserta
def addEdge(self, edge):
start, end = tuple(edge)
if end not in self.graph:
self.graph[end] = [] # no existe nodo destino, se crea
if start in self.graph:
if end not in self.graph[start]:
self.graph[start].append(end)
else:
self.graph[start] = [end] # no existe nodo origen, se crea
# Elimina un arco entre nodos
# El arco es una lista con los nodos que une
def removeEdge(self, edge):
start, end = tuple(edge)
if start in self.graph:
if end in self.graph[start]:
self.graph[start].remove(end)
# Devuelve una lista de los nodos aislados
def isolatedNodes(self):
return [n for n, e in self.graph.items() if self.inDegree(n) == 0]
# Semigrado exterior
def outDegree(self, node):
return len(self.graph[node])
# Semigrado interior
def inDegree(self, node):
return len([n for n, e in self.graph.items() if node != n and node in e])
Describimos a continuación los métodos de nuestra implementación. Los métodos que no aparecen serán los correspondientes a la clase base Graph().
- __init__(self, graph={})
-
Es el constructor del grafo.
Llamamos al constructor de la clase base para la creación del grafo.
- removeNode(self, node)
-
Elimina un nodo del grafo.
Si el nodo existe, se eliminan primero todas las referencias al nodo en las listas de adyacencia de los nodos precedentes a él. A continuación se elimina el nodo del diccionario.
Si el nodo no existe, se ignora la orden.
- addEdge(self, edge)
-
Inserta un arco entre los nodos indicados. El parámetro arco (edge) es una lista con el nodo origen y el nodo destino.
Al ser un grafo dirigido solo se añade el nodo destino en la lista de adyacencia del nodo origen.
Si no existe alguno de los nodos se inserta en el diccionario de la forma:
Si no existe el nodo destino se inserta con una lista de adyacencia vacía.
Si no existe el nodo origen se inserta con el nodo destino en su lista de adyacencia.
- removeEdge(self, edge)
-
Elimina un arco entre los nodos indicados. El parámetro arco (edge) es una lista con los nodos origen y destino, que están relacionados.
Se elimina de la lista de adyacencia del nodo origen el nodo de destino.
Si no existe alguno de los nodos, se ignora la orden.
- isoladedNodes(self)
-
Devuelve una lista con los nodos aislados del grafo.
Se considera aislado aquel nodo que no tiene referencias desde otros nodos, que no tiene arcos de entrada.
- outDegree(self, node)
- Devuelve el número de arcos a los nodos siguientes. La longitud de su lista de adyacencia.
- inDegree(self, node)
- Devuelve el número de arcos de los nodos precedentes. La longitud de la lista de nodos que contienen el nodo en su lista de adyacencia.
Construimos un script para probar nuestro módulo de tratamiento de grafos dirigidos. Los comentarios en cada sentencia son suficientemente descriptivos.
import grafo_dirigido as GRD
# Grafo ejemplo con listas de adyacencia
grafo = {'A': ['B', 'D'],
'B': ['C'],
'C': ['A', 'D'],
'D': []}
def testDirectedGraph():
g = GRD.DirectedGraph(grafo) #Crear el grafo con el diccionario de ejemplo
print('Grafo')
print(g) # Visualizar el grafo
print('Iteración')
for n in g: # Iterar sobre los nodos y arcos del grafo
print(n)
print(g.edges(n))
print('Nodos:', g.nodes()) # Visualizar todos los nodos
print('Arcos:', g.edges()) # Visualizar todos los arcos
print('Arcos desde el nodo C:', g.edges('C')) # Arcos desde un nodo
print('\nComprobaciones')
print('Vacío:', g.isEmpty()) # Comprobar si grafo vacío
print('Existe nodo A:', g.existNode('A')) # Comprobar si existe nodo
print('Existe nodo Z:', g.existNode('Z'))
print('Existe arco A-C:', g.existEdge(['A', 'C'])) # Comprobar arco
print('Existe arco A-Z:', g.existEdge(['A', 'Z']))
print('\nAñadir nodos y arcos')
g.addNode('E') # Añadir nodo
g.addEdge(('A', 'E')) # Añadir arco
g.addNode('F')
g.addEdge(('B', 'G'))
g.addEdge(('B', 'F'))
print('Grafo resultante')
print(g)
print('Medidas')
print('Grado de B:', g.degree('B')) # Obtener grado de un nodo
print('Grado de D:', g.degree('D'))
print('Grado de salida A:', g.outDegree('A')) #Semigrado exterior
print('Grado de entrada A:', g.inDegree('A')) #semigrado interior
print('Delta:', g.Delta()) # Obtener Delta del grafo
print('Orden:', g.order()) # Obtener orden
print('Tamaño:', g.size()) # Obtener tamaño
print('\nRecorridos')
print("DFS('A'):", g.DFS('A')) # Recorrido DFS
print("BFS('A'):", g.BFS('A')) # Recorrido BFS
# Obtener todos los caminos posibles entre dos nodos
print('Caminos de A a C:', g.findPaths('A', 'C'))
# Obtener el camino más corto entre dos nodos
print('Más corto de A a C:', g.shortestPath('A', 'C'))
print('\nEliminar arcos y nodos')
g.removeNode('C') # Eliminar nodo
g.removeEdge(['A', 'D']) # Eliminar arco
g.removeNode('Z') # Eliminar nodo inexistente
g.removeEdge(['B', 'Z']) # Eliminar arco inexistente
print('Grafo resultante')
print(g)
print('Nodos aislados:', g.isolatedNodes()) # Visualizar nodos aislados
if __name__ == '__main__':
testDirectedGraph()
El resultado de la ejecución del programa de prueba es:
Grafo
A: ['B', 'D']
B: ['C']
C: ['A', 'D']
D: []
Iteración
A
[('A', 'B'), ('A', 'D')]
B
[('B', 'C')]
C
[('C', 'A'), ('C', 'D')]
D
[]
Nodos: ['A', 'B', 'C', 'D']
Arcos: [('A', 'B'), ('A', 'D'), ('B', 'C'), ('C', 'A'), ('C', 'D')]
Arcos desde el nodo C: [('C', 'A'), ('C', 'D')]
Comprobaciones
Vacío: False
Existe nodo A: True
Existe nodo Z: False
Existe arco A-C: True
Existe arco A-Z: False
Añadir nodos y arcos
Grafo resultante
A: ['B', 'D', 'E']
B: ['C', 'G', 'F']
C: ['A', 'D']
D: []
E: []
F: []
G: []
Medidas
Grado de B: 3
Grado de D: 0
Grado de salida A: 3
Grado de entrada A: 1
Delta: 3
Orden: 7
Tamaño: 8
Recorridos
DFS('A'): ['A', 'E', 'D', 'B', 'F', 'G', 'C']
BFS('A'): ['A', 'B', 'D', 'E', 'C', 'G', 'F']
Caminos de A a C: [['A', 'B', 'C']]
Más corto de A a C: ['A', 'B', 'C']
Eliminar arcos y nodos
Grafo resultante
A: ['B', 'E']
B: ['G', 'F']
D: []
E: []
F: []
G: []
Nodos aislados: ['A', 'D']
6.5 Grafo ponderado
Los grafos ponderados son grafos con las aristas etiquetadas con un valor numérico o peso. Esa etiqueta puede ser una distancia, un tiempo o cualquier otro parámetro que resulte interesante definir en el grafo.
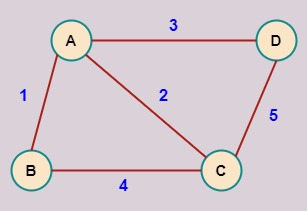
Grafo ponderado
Para la representación del grafo ponderado de la imágen, como un diccionario de Python, incluimos en las listas de adyacencia el peso de cada arco como una tupla de la forma nodo destino, peso, así:
grafo = {'A': [('B', 1), ('C', 2), ('D', 3)],
'B': [('A', 1), ('C', 4)],
'C': [('A', 2), ('B', 4), ('D', 5)],
'D': [('A', 3), ('C', 5)]}
Como los arcos en los grafos ponderados son bidireccionales, al igual que en los grafos no dirigidos, vemos que el nodo A contiene en su lista el nodo B, y en el nodo B aparece también el nodo A.
Vamos realizar la implementación empleando la clase Graph() que creamos al principio de este capítulo. Haremos uso de la herencia de los métodos correspondientes de la clase Graph(), reescribiendo aquellos métodos que no tenían en cuenta la existencia del peso asociado a los arcos.
# Grafo ponderado
# los arcos son bidireccionales, con peso único
import grafo as GR
class WeightedGraph(GR.Graph):
# Constructor, por defecto crea un diccionario vacío
# El grafo se presenta como un diccionario de la forma
# {nodo: [arcos]}
# arcos es una lista de tuplas de la forma (nodo_destino, peso)
def __init__(self, graph={}):
super().__init__(graph)
# Devuelve el número de arcos del grafo
def size(self):
arcs = []
for node, edges in self.graph.items():
for edge, w in edges:
sorted_edge = sorted([node, edge])
if sorted_edge not in arcs:
arcs.append(sorted_edge)
return len(arcs)
# Elimina un nodo del grafo
# Primero elimina todos los arcos del nodo
def removeNode(self, node):
if node in self.graph:
edges = list(self.graph[node])
for edge, w in edges:
self.removeEdge((node, edge))
self.graph.pop(node)
# Inserta una arco entre los nodos indicados
# El arco es una lista con los nodos que une
# Si no existe el nodo lo inserta
def addEdge(self, edge, weight):
n1, n2 = tuple(edge)
for n, e in [(n1, n2), (n2, n1)]:
if n in self.graph:
if e not in self.graph[n]:
self.graph[n].append((e, weight))
if n == e:
break # es un lazo
else:
self.graph[n] = [(e, weight)]
# Elimina una arco entre nodos
# El arco es una lista con los nodos que une
def removeEdge(self, edge):
n1, n2 = tuple(edge)
for n, e in [(n1, n2), (n2, n1)]:
if n in self.graph:
for node, weight in self.graph[n]:
if node == e:
self.graph[n].remove((node, weight))
# Recorrido en profundidad (Depth First Search)
def DFS(self, node):
visited = [node]
stack = [node]
while stack:
current = stack.pop()
if current not in visited:
visited.append(current)
for e, _ in self.graph[current]: # para cada nodo adyacente
if e not in visited:
stack.append(e)
return visited
# Recorrido en anchura (Breadth-First Search)
def BFS(self, node):
visited = [node]
queue = [node]
while queue:
current = queue.pop(0)
if current not in visited:
visited.append(current)
for e, _ in self.graph[current]: # para cada nodo adyacente
if e not in visited:
queue.append(e)
return visited
# Devuelve todos los caminos entre dos nodos
def findPaths(self, start, end, path = []):
if start not in self.graph or end not in self.graph:
return []
path = path + [start]
if start == end:
return [path]
paths = []
for node, _ in self.graph[start]: # para cada nodo adyacente
if node not in path:
newpaths = self.findPaths(node, end, path)
for subpath in newpaths:
paths.append(subpath)
return paths
# Devuelve el camino más corto entre dos nodos
# camino más corto == el de menor peso
# Algoritmo de Dijkstra para grafos ponderados
# https://www.teachyourselfpython.com/challenges.php?a=01_Solve_and_Learn&t=7-Sorting_Searching_Algorithms&s=02c_Dijkstras_Algorithm
def shortestPath(self, start, end):
INF = float('inf')
# Diccionario de nodos con un peso infinito
unvisited = {node: INF for node in self.graph.keys()}
# Diccionario de predecesores
predecessor = {node: node for node in self.graph.keys()}
visited = {}
current = start
currentWeight = 0
unvisited[current] = currentWeight # nodo origen peso 0
while True:
for node, weight in self.graph[current]:
if node not in unvisited:
continue # nodo ya tratado
newWeight = currentWeight + weight
if unvisited[node] > newWeight:
# Tomar el nodo con el menor peso
unvisited[node] = newWeight
predecessor[node] = current # predecesor con el menor peso
visited[current] = currentWeight # visitado con el menor peso
unvisited.pop(current) # eliminar de los no visitados
if not unvisited:
break # Terminar el bucle si no hay nodos por visitar
# Tomar el nodo con el menor peso de los no visitados
candidates = [(n, w) for n, w in unvisited.items() if w != INF]
current, currentWeight = sorted(candidates, key = lambda x: x[1])[0]
# Reconstrucción del camino de longitud mínima
# Se parte del nodo final al inicial
path = []
node = end
while True:
path.append(node)
if(node == predecessor[node]):
break
node = predecessor[node]
# Devuelve una tupla con el camino y el peso total
return (path[::-1], visited[end])
Describimos a continuación los métodos de nuestra implementación. Los métodos que no aparecen serán los correspondientes a la clase base Graph().
- __init__(self, graph={})
-
Es el constructor del grafo.
Llamamos al constructor de la clase base para la creación del grafo.
- size(self)
-
Devuelve el número de arcos del grafo.
Debemos tener en cuenta que la estructura de la lista de adyacencia del grafo incluye también el peso del arco.
- removeNode(self, node)
-
Elimina un nodo del grafo.
Debemos tener en cuenta que la estructura de la lista de adyacencia del grafo incluye también el peso del arco.
Si el nodo existe, se eliminan primero todas las referencias al nodo en las listas de adyacencia de los demás nodos. A continuación se elimina el nodo del diccionario.
Si el nodo no existe, se ignora la orden.
- addEdge(self, edge, weight)
-
Inserta un arco con su peso (weight) entre los nodos indicados. El parámetro arco (edge) es una lista con los nodos que están relacionados.
Al ser un grafo no dirigido se crean arcos entre ambos nodos.
Si no existe alguno de los nodos se inserta en el diccionario con el otro nodo en su lista de adyacencia.
- removeEdge(self, edge)
-
Elimina un arco entre los nodos indicados. El parámetro arco (edge) es una lista con los nodos que están relacionados.
Debemos tener en cuenta que la estructura de la lista de adyacencia del grafo incluye también el peso del arco.
Se elimina de la lista de adyacencia de cada nodo el otro nodo al que está conectado.
- DFS(self, node)
-
Devuelve el recorrido en profundidad (Depth First Search) del grafo a partir del nodo indicado.
Debemos tener en cuenta que la estructura de la lista de adyacencia del grafo incluye también el peso del arco.
El recorrido comienza en un nodo del grafo y se comprueba a todo lo largo de cada arco antes de retroceder.
Se hace uso de una pila para almacenar los nodos pendientes de tratar.
- BFS(self, node)
-
Devuelve el recorrido en anchura (Breadth First Search) del grafo a partir del nodo indicado.
Debemos tener en cuenta que la estructura de la lista de adyacencia del grafo incluye también el peso del arco.
Comienza en un nodo del grafo y comprueba los nodos adyacentes en el nivel del nodo, antes de pasar al siguiente nivel del grafo.
Se hace uso de una cola para almacenar los nodos pendientes de tratar.
- findPaths(self, start, end, path = [])
-
Devuelve una lista de listas con todos los caminos existentes entre los nodos inicio (start) y fin (end).
Debemos tener en cuenta que la estructura de la lista de adyacencia del grafo incluye también el peso del arco.
- shortestPath(self, start, end)
-
Devuelve el camino de menor peso entre los nodos inicio (start) y fin (end). Se entiende por menor peso el camino cuya suma de pesos de los arcos sea menor.
Reescribiremos el método implementando el algoritmo de Dijkstra. La idea subyacente en este algoritmo consiste en ir explorando todos los caminos más cortos que parten del nodo origen y que llevan a todos los demás nodos. El método devuelve una tupla con el camino entre el nodo origen y el destino, y el peso resultante para ese camino.
El algoritmo de Dijkstra fue concebido por el informático Edsger W. Dijkstra en 1958 y publicado tres años después. Este algoritmo no funciona en grafos ponderados con arcos de coste negativo.
Construimos un script para probar nuestro módulo de tratamiento de grafos ponderados. Los comentarios en cada sentencia son suficientemente descriptivos.
import grafo_ponderado as GRP
# Grafo ejemplo con listas de adyacencia y pesos asociados
grafo = {'A': [('B', 1), ('C', 2), ('D', 3)],
'B': [('A', 1), ('C', 4)],
'C': [('A', 2), ('B', 4), ('D', 5)],
'D': [('A', 3), ('C', 5)]}
def testGrafo():
g = GRP.WeightedGraph(grafo) # Crear el grafo con el diccionario de ejemplo
print('Grafo')
print(g) # Visualizar el grafo
print('Iteración')
for n in g: # Iterar sobre los nodos y arcos del grafo
print(n)
print(g.edges(n))
print('Nodos:', g.nodes()) # Visualizar todos los nodos
print('Arcos:', g.edges()) # Visualizar todos los arcos
print('Arcos desde el nodo C:', g.edges('C')) # Arcos desde un nodo
print('\nComprobaciones')
print('Vacío:', g.isEmpty()) # Comprobar si grafo vacío
print('Existe nodo A:', g.existNode('A')) # Comprobar si existe nodo
print('Existe nodo Z:', g.existNode('Z'))
print('Existe arco A-C:', g.existEdge(['A', 'C'])) # Comprobar arco
print('Existe arco A-Z:', g.existEdge(['A', 'Z']))
print('\nAñadir nodos y arcos')
g.addNode('E') # Añadir nodo
g.addEdge(('A', 'E'), 6) # Añadir arco con el peso
g.addEdge(('B', 'F'), 4)
g.addEdge(('B', 'G'), 5)
print('Grafo resultante')
print(g)
print('Medidas')
print('Grado de B:', g.degree('B')) # Obtener grado de un nodo
print('Grado de D:', g.degree('D'))
print('Delta:', g.Delta()) # Obtener Delta del grafo
print('Orden:', g.order()) # Obtener orden
print('Tamaño:', g.size()) # Obtener tamaño
print('\nRecorridos')
print("DFS('A'):", g.DFS('A')) # Recorrido DFS
print("BFS('A'):", g.BFS('A')) # Recorrido BFS
# Obtener todos los caminos posibles entre dos nodos
print(g.findPaths('A', 'C'))
# Obtener el camino más corto entre dos nodos
path, weight = g.shortestPath('D', 'G')
print(f'Dijkstra: ruta D-G:{path} peso:{weight}')
print('\nEliminar arcos y nodos')
g.removeEdge(['D', 'A']) # Eliminar arco
g.removeNode('C') # Eliminar nodo
print('Grafo resultante')
print(g)
print('Nodos aislados:', g.isolatedNodes()) # Visualizar nodos aislados
if __name__ == '__main__':
testGrafo()
El resultado de la ejecución del programa de prueba es:
Grafo
A: [('B', 1), ('C', 2), ('D', 3)]
B: [('A', 1), ('C', 4)]
C: [('A', 2), ('B', 4), ('D', 5)]
D: [('A', 3), ('C', 5)]
Iteración
A
[('A', ('B', 1)), ('A', ('C', 2)), ('A', ('D', 3))]
B
[('B', ('A', 1)), ('B', ('C', 4))]
C
[('C', ('A', 2)), ('C', ('B', 4)), ('C', ('D', 5))]
D
[('D', ('A', 3)), ('D', ('C', 5))]
Nodos: ['A', 'B', 'C', 'D']
Arcos: [('A', ('B', 1)), ('A', ('C', 2)), ('A', ('D', 3)), ('B', ('A', 1)), ('B', ('C', 4)), ('C', ('A', 2)), ('C', ('B', 4)), ('C', ('D', 5)), ('D', ('A', 3)), ('D', ('C', 5))]
Arcos desde el nodo C: [('C', ('A', 2)), ('C', ('B', 4)), ('C', ('D', 5))]
Comprobaciones
Vacío: False
Existe nodo A: True
Existe nodo Z: False
Existe arco A-C: False
Existe arco A-Z: False
Añadir nodos y arcos
Grafo resultante
A: [('B', 1), ('C', 2), ('D', 3), ('E', 6)]
B: [('A', 1), ('C', 4), ('F', 4), ('G', 5)]
C: [('A', 2), ('B', 4), ('D', 5)]
D: [('A', 3), ('C', 5)]
E: [('A', 6)]
F: [('B', 4)]
G: [('B', 5)]
Medidas
Grado de B: 4
Grado de D: 2
Delta: 4
Orden: 7
Tamaño: 8
Recorridos
DFS('A'): ['A', 'E', 'D', 'C', 'B', 'G', 'F']
BFS('A'): ['A', 'B', 'C', 'D', 'E', 'F', 'G']
[['A', 'B', 'C'], ['A', 'C'], ['A', 'D', 'C']]
Dijkstra: ruta D-G:['D', 'A', 'B', 'G'] peso:9
Eliminar arcos y nodos
Grafo resultante
A: [('B', 1), ('E', 6)]
B: [('A', 1), ('F', 4), ('G', 5)]
D: []
E: [('A', 6)]
F: [('B', 4)]
G: [('B', 5)]
Nodos aislados: ['D']
