Árboles
5 Árboles
Los árboles presentan una estructura jerárquica no lineal, distinta a las estructuras vistas hasta ahora.
- Los elementos, o nodos, se relacionan con una estructura jerárquica más compleja y flexible que la relación de orden.
- Hay un elemento distinguido, el raíz, y los demás se dividen en subárboles, y así recursivamente.
- Cada elemento, excepto el raíz, tiene un padre superior y cero o más hijos subordinados.
- A diferencia de la relación de orden, no existe una única forma de recorrer los elementos, sino varias: in-orden, pre-orden, post-orden y por niveles.
Los árboles tienen una terminología específica:
- Nodo (Node). Cada uno de los elementos de un árbol con información. Cada nodo puede tener cero o más hijos.
- Raiz (root). Es el nodo principal. No tiene antecedentes.
- Padre (parent). Es el nodo que tiene al menos un descendiente.
- Hijo (children). Nodo que está directamente bajo otro nodo.
- Hermano (sibling). Nodos que tienen el mismo padre.
- Hoja (leave) o terminal. Nodos que no tienen ningún descendiente.
- Subárbol (subtree).Conjunto de descendientes de un nodo por una de sus ramas.
- Descendiente o sucesor (descendant or successor). Nodos que están inmediatamente debajo de otro nodo.
- Antecedente o antecesor (predecesor or ancestor). Nodo del que dependen otros nodos.
- Interior. Nodo que tiene al menos un descendiente.Es un nodo no terminal.
- Grado (degree). Número de descendientes directos de un nodo interior.
- Arista (edge). Línea que une dos nodos, padre con hijo.
- Nivel (level). Número de aristas que hay que recorrer para llegar a un nodo desde la raíz mas uno.
- Anchura (width). Número de nodos que hay en un nivel.
- Profundidad o altura (height). Número máximo de nodos de una rama del árbol. Es igual al nivel más alto de los nodos del árbol.
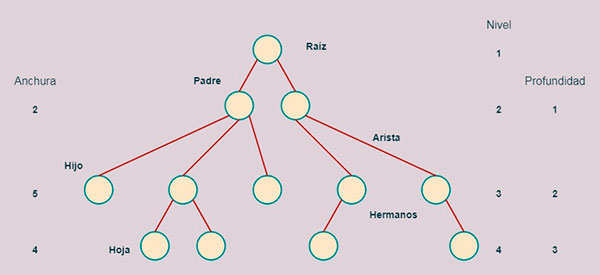
Árbol
5.1 Árbol binario
Los árboles binarios son una categoría especial del árbol que consta de un nodo raíz que tiene dos subárboles binarios denominados subárbol izquierdo y subárbol derecho. Esta es una definición recursiva, ya que cada subárbol es a su vez un árbol binario.
Existen diferentes tipos de arboles binarios:
- Full Binary Tree. Si cada nodo tiene 0 o 2 hijos.
- Complete Binary Tree. Si todos los niveles están completamente llenos excepto posiblemente el ultimo nivel y el ultimo nivel tiene todos los nodos a la izquierda.
- Perfect Binary Tree. Cuando todos los nodos internos tienen dos hijos y todos los nodos hojas tiene el mismo nivel.
- Balanced Binary Tree. La diferencia de alturas de los subárboles izquierdo y derecho no es superior a 1.
- Degenerate (pathological) Tree. Árbol donde todos los nodos internos tienen un hijo.
Los árboles binarios son útiles para almacenar datos de forma organizada, de modo que puedan recuperarse, insertarse, actualizarse y eliminarse rápidamente. La disposición de los nodos permite que cada comparación se salte aproximadamente la mitad del resto del árbol, por lo que toda la búsqueda es muy rápida.
5.1.1 Recorridos
El recorrido de un árbol binario es un proceso en profundidad, donde se visitan todos los nodos. Como cada nodo representa un subárbol en sí mismo es fácil hacer uso de la recursividad para realizar el recorrido.
Se consideran dos tipos de recorrido: recorrido en profundidad y recorrido en anchura o a nivel. Puesto que los árboles no son secuenciales como las listas, hay que buscar estrategias alternativas para visitar todos los nodos.
- En profundidad (Depth-first).
- Pre-order
- In-order
- Post-order
- En anchura (Breadth-first).
- Level order
5.1.1.1 Pre-orden
En este método de recorrido primero se visita el nodo raíz, luego el subárbol izquierdo y finalmente el subárbol derecho.
- Se visita la raíz.
- Se recorre en pre-orden el subárbol izquierdo.
- Se recorre en pre-orden el subárbol derecho.
El algoritmo de recorrido del árbol preordenado recibe su nombre del orden en que se obtienen los nodos. Primero el nodo raíz. A continuación, el hijo izquierdo del nodo. Y, por último el hijo derecho del nodo. En este proceso recursivo el hijo derecho de un nodo sólo se visita cuando todos los nodos del subárbol izquierdo del nodo actual y el propio nodo actual ya han sido recorridos.
El recorrido en pre-orden produce una notación prefija.
5.1.1.2 In-orden/orden central
En este método de recorrido se visita primero el subárbol de la izquierda, luego la raíz y después el subárbol de la derecha.
- Se recorre en in-orden el subárbol izquierdo.
- Se visita la raíz.
- Se recorre en in-orden el subárbol derecho.
El recorrido en orden central produce una notación convencional.
5.1.1.3 Post-orden
En este método de recorrido el nodo raíz se visita en último lugar, de ahí su nombre. Primero se recorre el subárbol izquierdo, luego el derecho y finalmente el nodo raíz.
- Se recorre en post-orden el subárbol izquierdo.
- Se recorre en post-orden el subárbol derecho.
- Se visita la raíz.
El recorrido en post-orden produce una notación postfija.
5.1.1.4 Por niveles
El recorrido por niveles es una técnica de recorrido del árbol binario que se basa en la amplitud. Primero se recorre un nodo. A continuación, recorremos todos los nodos vecinos en ese nivel antes de pasar a los nodos del siguiente nivel del árbol, de ahí lo de recorrido por niveles. Este proceso continúa hasta que se visitan todos los nodos del árbol.
- Primero se visita el elemento del nivel 0 (la raíz).
- Se pasa al siguiente nivel, recorriendolo de izquierda a derecha.
- Se repite el paso 2 con todos los niveles.
En este caso el recorrido no se realizará de forma recursiva sino iterativa, utilizando una cola como estructura de datos auxiliar. El procedimiento consiste en encolar los subárboles izquierdo y derecho del nodo extraido de la cola, y seguir desencolando y encolando hasta que la cola esté vacía.
5.2 Árbol de búsqueda binario
Los árboles de búsqueda binaria (Binary Search Tree - BST) son una categoría especial del árbol binario que tienen unas propiedades específicas de asignación de los elementos dentro del árbol.
- Todos los nodos del subárbol izquierdo son menores que el nodo raíz.
- Todos los nodos del subárbol derecho son mayores que el nodo raíz.
- Los dos subárboles de cada nodo son también BST.
A partir de ahora solo trataremos los árboles binarios ordenados, por lo que emplearemos el término árbol en este sentido.
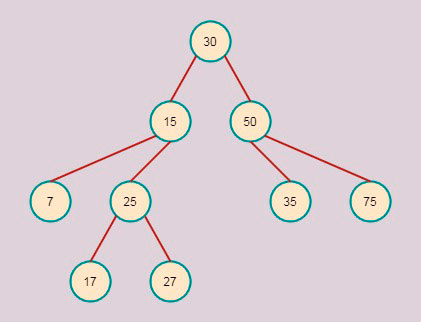
Árbol binario (BST)
Ventajas de un BST:
- Cuando está equilibrado, un BST proporciona inserciones, eliminaciones y búsquedas de manera muy eficiente y su código es más sencillo que el de otras estructuras de datos.
Contras de un BST:
- Es lento para una búsqueda de fuerza bruta. Cuando se necesita iterar sobre cada nodo, es más rápido emplear una lista.
- La forma del árbol de búsqueda binario depende totalmente del orden de las inserciones, y puede degenerar.
- Cuando el árbol se desequilibra, todas las operaciones se degradan rápidamente.
- Dado que normalmente se trata de punteros a objetos complejos, un BST puede requerir bastante más memoria que una lista, aunque esto depende de la implementación.
Casi todas las bases de datos existentes utilizan BST para el almacenamiento y la búsqueda de claves. Así, cuando se crea una clave primaria, lo que realmente ocurre es que se crea un árbol binario donde las claves son los valores de la columna, y esos nodos apuntan a filas de la base de datos. Esto permite buscar rápidamente filas de la base de datos proporcionando una clave
Las operaciones habituales sobre los árboles binarios son:
| Método | Descripción |
|---|---|
| insert() | Inserta un nuevo nodo en la posición correcta dentro del BST. |
| delete() | Encuentra un nodo basado en su valor y lo elimina del árbol. |
| getMin() | Búsca y devuelve el elemento con el menor valor. |
| getMax() | Búsca y devuelve el elemento con el mayor valor. |
| exists() | Realiza una búsqueda binaria en el árbol para encontrar un nodo específico basado en su valor. Devuelve True si lo encuentra y False en caso contrario. |
| inOrder() | Realiza y muestra el resultado de un recorrido en orden del árbol. |
| preOrder() | Realiza y muestra el resultado de un recorrido pre-orden del árbol. |
| postOrder() | Realiza y muestra el resultado de un recorrido post-orden del árbol. |
| levelOrder() | Realiza y muestra el resultado de un recorrido por niveles del árbol. |
| drawTree() | Devuelve una representación del árbol de una forma gráfica símple. |
Dispondremos además de los métodos especiales:
| Método | Descripción |
|---|---|
| __init__(self) | Constructor, crea un nodo del árbol vacío. |
| __repr__(self) | Devuelve una representación gráfica símple del árbol. |
| __len__(self) | Devuelve el tamaño del árbol. |
La inserción en un árbol binario de búsqueda tiene la ventaja sobre las listas ordenadas que no necesita hacer una reubicación de los elementos de la estructura para que esta siga ordenada después de la inserción. En la inserción basta con ir avanzando por el árbol escogiendo la rama izquierda o derecha en función del valor que se inserta y el del nodo actual, hasta encontrar su ubicación
El borrado es la operación más complicada, ya que el árbol debe seguir siendo BST después de borrar un nodo. Pueden darse tres casos:
- El nodo no tiene descendientes, con lo que se borra.
- El nodo tiene al menos un descendiente por una sola rama. Se borra dicho nodo, y su primer descendiente se asigna como hijo del padre del nodo borrado.
- El nodo tiene al menos un descendiente por cada rama. Al borrar dicho nodo es necesario mantener la coherencia de los enlaces, y que el árbol siga siendo BST. Para ello se sustituye la información del nodo que se borra por el de una de las hojas, borrando a continuación dicha hoja.
Crearemos una clase con los métodos necesarios para implementar nuestro árbol binario. Como en un árbol binario los subarboles son a su vez arboles binarios vamos a hacer uso de la recursividad en nuestra implementación.
En el recorrido por niveles, el método levelOrder(), hace uso de una cola, por lo que vamos a importar la versión que desarrollamos en el punto sobre Cola basada en listas.
# Binary Search Tree/Árbol de búsqueda binario
import cola as Q
class BinarySearchTree:
# Nodo
def __init__(self, value=None, left=None, right=None):
self.value = value
self.left = left
self.right = right
def __repr__(self):
output = self.drawTree([])
return "\n".join(map(str, output))
def __len__(self):
if self == None:
return 0
else:
size = 1
if self.right:
size += self.right.__len__()
if self.left:
size += self.left.__len__()
return size
def insert(self, value):
if self.value:
if value < self.value:
# Rama izquierda
if self.left is None:
self.left = BinarySearchTree(value)
else:
self.left.insert(value)
elif value > self.value:
# Rama derecha
if self.right is None:
self.right = BinarySearchTree(value)
else:
self.right.insert(value)
else:
self.value = value
def delete(self, value):
if self == None:
return self
if value < self.value:
if self.left:
self.left = self.left.delete(value)
return self
if value > self.value:
if self.right:
self.right = self.right.delete(value)
return self
if self.right == None:
return self.left
if self.left == None:
return self.right
min_larger_node = self.right
while min_larger_node.left:
min_larger_node = min_larger_node.left
self.value = min_larger_node.value
self.right = self.right.delete(min_larger_node.value)
return self
def getMin(self):
curr = self
while curr.left is not None:
curr = curr.left
return curr.value
def getMax(self):
curr = self
while curr.right is not None:
curr = curr.right
return curr.value
def exists(self, value):
if value == self.value:
return True
if value < self.value:
if self.left == None:
return False
return self.left.exists(value)
if self.right == None:
return False
return self.right.exists(value)
def inOrder(self, output):
# Recorrido izquierda, raíz, derecha
if self.left is not None:
# Izquierda
self.left.inOrder(output)
if self.value is not None:
# Raíz
output.append(self.value)
if self.right is not None:
# Derecha
self.right.inOrder(output)
return output
def preOrder(self, output):
# Recorrido raíz, izquierda, derecha
if self.value is not None:
# Raíz
output.append(self.value)
if self.left is not None:
# Izquierda
self.left.preOrder(output)
if self.right is not None:
# Derecha
self.right.preOrder(output)
return output
def postOrder(self, output):
# Recorrido izquierda, derecha, raíz
if self.left is not None:
# Izquierda
self.left.postOrder(output)
if self.right is not None:
# Derecha
self.right.postOrder(output)
if self.value is not None:
# Raíz
output.append(self.value)
return output
def levelOrder(self, output):
# Recorrido por niveles
if self == None:
return output
# Se hace uso de una cola
q = Q.Cola()
q.enqueue(self)
while not q.isEmpty():
node = q.dequeue()
if node is None:
continue
output.append(node.value)
q.enqueue(node.left)
q.enqueue(node.right)
return output
def drawTree(self, output, level=0):
# Se recorre derecha, raíz, izquierda
if self.right is not None:
self.right.drawTree(output, level + 1)
if self.value is not None:
output.append(' ' * 4 * level + f'::{self.value}')
if self.left is not None:
self.left.drawTree(output, level + 1)
return output
Describimos a continuación los métodos de nuestra implementación.
En la clase BinarySearchTree:
- __init__(self)
- El constructor del árbol crea un nodo vacío con los campos valor (value) y enlace a ramas izquierda (left) y derecha (right) a nulo.
- __repr__(self)
- El método de representación del árbol de una forma gráfica simple.
Hace uso del método auxiliar drawTree(). El resultado es extremadamente simple, pero permite observar los niveles y las ramas con los valores de cada nodo.
- __len__(self)
- El método que devuelve el tamaño del árbol.
- insert(self, value)
- Es el método para añadir un nodo al árbol. Le pasamos el dato que va a contener el nodo para que lo pase al constructor del nuevo nodo.
Se recorren los nodos recursivamente buscando la rama izquierda o derecha dependiendo del valor del nodo nuevo.
- delete(self, value)
- Método para eliminar un nodo del árbol.
Se ajustan los nodos que dependan del nodo borrado manteniendo la regla izquierda/derecha del orden de los nodos según su valor.
- getMin(self)
- Método que devuelve valor menor almacenado en el árbol. Recorre la rama izquierda hasta llegar a la hoja.
- getMax(self)
- Método que devuelve valor mayor almacenado en el árbol. Recorre la rama derecha hasta llegar a la hoja.
- exists(self, value)
- Método para verificar la existencia de un valor en el árbol. Devuelve True si el valor existe y False en caso contrario.
- inOrder(self, output)
- Método que devuelve un recorrido del árbol en orden central. Se visita primero el subárbol de la izquierda, luego la raíz y después el subárbol de la derecha.
- preOrder(self, output)
- Método que devuelve un recorrido del árbol en preorden. Se visita primero la raíz, luego el subárbol de la izquierda, y después el subárbol de la derecha.
- postOrder(self, output)
- Método que devuelve un recorrido del árbol en postorden. Se visita primero el subárbol de la izquierda, luego el subárbol de la derecha y después la raíz.
- levelOrder(self, output)
- Método que devuelve un recorrido del árbol por niveles. Se visita nivel por nivel, recorriendo los niveles de izquierda a derecha.
Se hace uso de una cola para almacenar los hijos izquierda/derecha de cada nodo.
Método auxiliar.
- drawTree(self, output, level=0)
- Crea una representación textual del árbol.
El método especial __repr__() hace uso de este método.
Devuelve una representación del árbol en apaisado. Girando el resultado impreso es relativamente fácil ver la estructura del árbol. (Si no es un árbol grande y se tiene suficiente imaginación).
Construimos un script para probar nuestro módulo de árboles de búsqueda binarios. Los textos en las sentencias de salida son suficientemente descriptivos.
import binary_search_tree as BST
def testBinarySearchTree():
bst = BST.BinarySearchTree()
data = [30, 50, 15, 25, 17, 27, 75, 7, 35]
print("insert:", data)
for d in data:
bst.insert(d)
print("size:", len(bst))
print("in-order:", bst.inOrder([]))
print("pre-order:", bst.preOrder([]))
print("post-order:", bst.postOrder([]))
print("level-order:", bst.levelOrder([]))
print("tree:")
print(bst)
print("min:", bst.getMin())
print("max:", bst.getMax())
print("exist 25:", bst.exists(25))
print("exist 33:", bst.exists(33))
data = [5, 25, 50]
print("delete:", data)
for d in data:
bst.delete(d)
print("size:", len(bst))
print("in-order:", bst.inOrder([]))
print("tree:")
print(bst)
if __name__ == '__main__':
testBinarySearchTree()
El resultado de la ejecución del programa de prueba es:
insert: [30, 50, 15, 25, 17, 27, 75, 7, 35]
size: 9
in-order: [7, 15, 17, 25, 27, 30, 35, 50, 75]
pre-order: [30, 15, 7, 25, 17, 27, 50, 35, 75]
post-order: [7, 17, 27, 25, 15, 35, 75, 50, 30]
level-order: [30, 15, 50, 7, 25, 35, 75, 17, 27]
tree:
::75
::50
::35
::30
::27
::25
::17
::15
::7
min: 7
max: 75
exist 25: True
exist 33: False
delete: [5, 25, 50]
size: 7
in-order: [7, 15, 17, 27, 30, 35, 75]
tree:
::75
::35
::30
::27
::17
::15
::7
